Benchmarking self-supervised methods for imaging without ground truth

Self-Supervised Machine Learning workshop, 24-25th Feb

Andrew Wang & Julián Tachella

Introduction

  • Aim: first benchmark of all SotA self-supervised methods for MRI reconstruction;
  • Aim: demo of self-supervised learning using DeepInverse library. Install using pip.

Find the full experiments with more comparisons in the paper: “Benchmarking Self-Supervised Methods for Accelerated MRI Reconstruction”, 2025.

Notes:

  • We assume that measurements are generated from multiple random operators that span the whole space as this is required for many of the algorithms.
  • We demonstrate feedforward methods \(\hat{x}=f_\theta(y)\) rather than generative models.
  • We assume noiseless data; some methods can be easily generalised to noisy scenarios.
import deepinv as dinv
import torch

device = dinv.utils.get_freer_gpu() if torch.cuda.is_available() else "cpu"
rng = torch.Generator(device=device).manual_seed(0)
results = {}

0. Define experiment training

First, define all common code for training (MRI physics, masking, model, data and metrics).

We provide many easy-to-use classes for MRI-related experiments. See Example - “Tour of MRI functionality in DeepInverse” for more.

We train with a custom FastMRI subset of 973 images created using deepinv.datasets.FastMRISliceDataset.save_simple_dataset (download here), and load it with deepinv.datasets.SimpleFastMRISliceDataset.

Note: by using this dataset, you confirm that you have agreed to and signed the FastMRI data use agreement.

file_name = "fastmri_knee_singlecoil.pt"

Define physics & model

Define MRI physics where each image is masked with a random Gaussian-weighted Cartesian mask at 4x acceleration. Define an unrolled MoDL network with a small UNet backbone (3 scales) and 3 unrolled iterations. See Example - “Tour of MRI functionality in DeepInverse” for other examples.

physics_generator = dinv.physics.generator.GaussianMaskGenerator(
    img_size=(128, 128), acceleration=4, rng=rng, device=device
)
physics = dinv.physics.MRI(img_size=(128, 128), device=device)

denoiser = dinv.models.UNet(2, 2, scales=3)
model = lambda: dinv.utils.demo.demo_mri_model(denoiser=denoiser, num_iter=3, device=device).to(device)

Define data

Define FastMRI small train and test datasets resized for speed, then simulate random k-space measurements using the physics, then load the generated measurements. We keep the test set at maximum 50 images for speed.

from torchvision.transforms import Resize
train_dataset = dinv.datasets.SimpleFastMRISliceDataset("data", file_name=file_name, transform=Resize(128), train=True, train_percent=0.8, download=True)
test_dataset = dinv.datasets.SimpleFastMRISliceDataset("data", file_name=file_name, transform=Resize(128), train=False, train_percent=0.8,)

path = dinv.datasets.generate_dataset(train_dataset=train_dataset, test_dataset=test_dataset, physics=physics, physics_generator=physics_generator, save_physics_generator_params=True, overwrite_existing=False, device=device, save_dir="data", batch_size=1)

train_dataset, test_dataset = dinv.datasets.HDF5Dataset(path, split="train", load_physics_generator_params=True), dinv.datasets.HDF5Dataset(path, split="test", load_physics_generator_params=True)
train_dataloader, test_dataloader = torch.utils.data.DataLoader(train_dataset, shuffle=True), torch.utils.data.DataLoader(torch.utils.data.Subset(test_dataset, range(min(len(test_dataset), 50))))
x, y, params = next(iter(test_dataloader))
dinv.utils.plot({
    "x": x,
    "y": y,
    "Mask": params["mask"],
    "Zero-filled": physics.A_adjoint(y, **params)
}, figsize=(15, 4))

Define trainer

def train(loss: dinv.loss.Loss, epochs: int = 0):
    _model = model()
        
    trainer = dinv.Trainer(
        model = _model,
        physics = physics,
        optimizer = torch.optim.Adam(_model.parameters(), lr=1e-3),
        train_dataloader = train_dataloader,
        eval_dataloader = test_dataloader,
        epochs = epochs,
        losses = loss,
        scheduler = None,
        metrics = dinv.metric.PSNR(complex_abs=True),
        ckp_interval = 10,
        device = device,
        eval_interval = 1,
        save_path = "models",
        plot_images = False,
        wandb_vis = False,
    )

    trainer.train()
    trainer.plot_images = True
    return trainer

1. Equivariant imaging methods

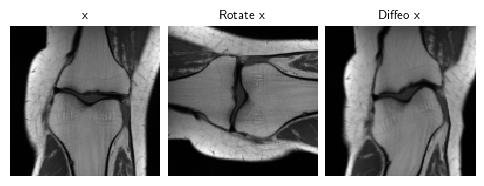
1a. Equivariant imaging (EI)

The EI self-supervised loss [1] assumes that the set of signals is invariant to a group of transformations in order to learn from incomplete measurement data alone:

\(\mathcal{L}_\text{EI}=\lVert T_g \hat{x} - f(A(T_g \hat{x}), A)\rVert_2^2\)

where \(\hat{x}=f(y, A)\) is a reconstructed signal and \(T_g\) is a transformation sampled at random from a group \(g\sim G\). EI was applied to MRI in [2]. Note that this works even when \(A\) is fixed across the dataset as it constructs multiple virtual operators.

Implementation: loss functions abstracted into EILoss(...), keeping a modular structure.

See also: Example - “Self-supervised learning with Equivariant Imaging for MRI”; Example - “Image transformations for Equivariant Imaging”; Docs - deepinv.loss.EILoss.

[1] Chen D., Tachella J. & Davies M., “Equivariant Imaging: Learning Beyond the Range Space”
[2] Chen D., Tachella J. & Davies M., “Robust Equivariant Imaging: a fully unsupervised framework for learning to image from noisy and partial measurements”

1a. Equivariant Imaging Results

loss = [
    dinv.loss.MCLoss(),
    dinv.loss.EILoss(transform=dinv.transform.Rotate())
]

# Set epochs > 0 to train the model
trainer = train(loss, epochs=0)

# Load pretrained model for 50 epochs, test on test dataset, and save sample reconstruction
trainer.load_model("models/pretrained/ei.pth.tar")

results["ei"] = trainer.test(test_dataloader)

physics.update_parameters(**params)
results["ei"]["sample"] = trainer.model(y, physics)

Test results:
PSNR no learning: 26.897 +- 2.730
PSNR: 30.643 +- 2.992

1b. Diffeomorphic-equivariant imaging

EI was extended beyond the Euclidean transformation group to the non-linear diffeomorphic group in [3] for MRI problems:

\(\mathcal{L}_\text{Diffeo-EI}=\mathcal{L}_\text{EI}\text{ where }G=\text{Diff}(\mathbb{R}^n)\)

See also: Example - “Image transforms for equivariance & augmentations”.

[3] Wang A. & Davies M., “Fully unsupervised dynamic MRI reconstruction”

dinv.utils.plot({"x": x, "Rotate x": dinv.transform.Rotate()(x), "Diffeo x": dinv.transform.CPABDiffeomorphism()(x)} figsize=(6, 2))

loss = [
    dinv.loss.MCLoss(),
    dinv.loss.EILoss(transform=dinv.transform.CPABDiffeomorphism(device=device))
]
# Set epochs > 0 to train the model
trainer = train(loss, epochs=0)
The model has 2070091 trainable parameters
# Load pretrained model for 50 epochs, test on test dataset, and save sample reconstruction
trainer.load_model("models/pretrained/diffeo-ei.pth.tar")

results["diffeo-ei"] = trainer.test(test_dataloader)

physics.update_parameters(**params)
results["diffeo-ei"]["sample"] = trainer.model(y, physics)

Test results:
PSNR no learning: 26.897 +- 2.730
PSNR: 31.388 +- 2.496

2. Multi-operator methods

2a. Multi-operator imaging (MOI)

The MOI self-supervised loss [4] can be used to learn when signals are observed via multiple (possibly incomplete) forward operators \(\{A_g\}_{g=1}^{G}\), i.e. \(y_i = A_{g_i}x_i\) where \(g_i\in \{1,\dots,G\}\). The loss is constructed as follows:

\(\mathcal{L}_\text{MOI}=\lVert\hat{x} - f(A_g\hat{x},A_g)\rVert_2^2\)

where \(\hat{x}=f(y,A_s)\) is a reconstructed signal (observed via operator \(A_s\)) and \(A_g\) is a forward operator sampled at random from a set \(\{A_g\}_{g=1}^{G}\).

See also: Example - “Self-supervised learning from incomplete measurements of multiple operators.”; Docs - deepinv.loss.MOILoss.

[4] Chen D., Tachella J. & Davies M., “Unsupervised Learning From Incomplete Measurements for Inverse Problems”

loss = [
    dinv.loss.MCLoss(),
    dinv.loss.MOILoss(physics_generator=physics_generator)
]
# Set epochs > 0 to train the model
trainer = train(loss, epochs=0)
The model has 2070091 trainable parameters
# Load pretrained model for 50 epochs, test on test dataset, and save sample reconstruction
trainer.load_model("models/pretrained/moi.pth.tar")

results["moi"] = trainer.test(test_dataloader)

physics.update_parameters(**params)
results["moi"]["sample"] = trainer.model(y, physics)

Test results:
PSNR no learning: 26.897 +- 2.730
PSNR: 31.260 +- 2.339

2b. Multi-operator equivariant imaging (MO-EI)

One can combine the multi-operator and equivariant imaging losses to leverage an even greater set of virtual operators (using notation from above), introduced in [5]:

\(\mathcal{L}_\text{MO-EI}=\lVert T_g\hat{x} - f(A_h(T_g \hat{x}), A_h)\rVert_2^2,\quad A_h\in\{A_h\}_{h=1}^{H},g\in G\)

where \(H\) is the set of operators and \(G\) is the group.

Because of the modularity of DeepInverse, this is very easily implemented. See also: Docs - deepinv.loss.MOEILoss.

[5] Wang A. & Davies M., “Benchmarking Self-Supervised Methods for Accelerated MRI Reconstruction”

loss = [
    dinv.loss.MCLoss(),
    dinv.loss.MOEILoss(transform=dinv.transform.CPABDiffeomorphism(device=device), physics_generator=physics_generator)
]
# Set epochs > 0 to train the model
trainer = train(loss, epochs=0)
The model has 2070091 trainable parameters
# Load pretrained model for 50 epochs, test on test dataset, and save sample reconstruction
trainer.load_model("models/pretrained/mo-ei.pth.tar")

results["mo-ei"] = trainer.test(test_dataloader)

physics.update_parameters(**params)
results["mo-ei"]["sample"] = trainer.model(y, physics)

Test results:
PSNR no learning: 26.897 +- 2.730
PSNR: 31.601 +- 2.326

3. Measurement splitting methods

3a. Self-supervised data undersampling (SSDU)

The SSDU measurement splitting loss [6,7,8] splits the measurement \(y\in\mathbb{R}^m\) and forward operator \(A\) into two smaller pairs \((y_1\in\mathbb{R}^{m_1},A_1)\) and \((y_2\in\mathbb{R}^{m_2},A_2)\) to compute the self-supervised loss:

\(\mathcal{L}_\text{SSDU}=\frac{m}{m_2}\lVert y_2 - A_2 f(y_1,A_1)\rVert_2^2\)

where \(f\) is the network, \(A_1 = M_1A, A_2 = M_2A\), and \(M_i\) are randomly generated masks (i.e. diagonal matrices) such that \(M_1+M_2=\mathbb{I}_m\). At inference-time, SSDU simply uses the full measurements \(\hat x=f(y,A)\).

See also: Example - “Self-supervised learning with measurement splitting”.

[6] Yaman B. et al., “SSDU”
[7] Liu J. et al., “RARE: Image Reconstruction using Deep Priors Learned without GT”
[8] Eldeniz C. et al., “Phase2Phase…”

mask_generator = dinv.physics.generator.GaussianSplittingMaskGenerator((2, 128, 128), split_ratio=0.6, device=device, rng=rng)
loss = dinv.loss.SplittingLoss(mask_generator=mask_generator, eval_split_input=False)
# Set epochs > 0 to train the model
trainer = train(loss, epochs=0)
The model has 2070091 trainable parameters
# Load pretrained model for 50 epochs, test on test dataset, and save sample reconstruction
trainer.load_model("models/pretrained/ssdu.pth.tar")

results["ssdu"] = trainer.test(test_dataloader)

physics.update_parameters(**params)
results["ssdu"]["sample"] = trainer.model(y, physics)

Test results:
PSNR no learning: 26.897 +- 2.730
PSNR: 26.796 +- 2.191

3b. SSDU with test-time Monte Carlo

We can extend SSDU [6] during inference-time by averaging the model over multiple realizations of the random splitting, i.e.

\(\hat{x} = \frac{1}{N}\sum_{i=1}^N f(y_1^{(i)},A_1^{(i)})\)

where \(N\) is the number of Monte-Carlo samples. The training loss function remains the same as SSDU. This was proposed in [9] for CT denoising, and has shown promising results in [3].

[9] Hendriksen A., Pelt D., Batenburg K., “Noise2Inverse: Self-supervised deep convolutional denoising for tomography”

loss = dinv.loss.SplittingLoss(mask_generator=mask_generator, eval_split_input=True, eval_n_samples=20)
# Set epochs > 0 to train the model
trainer = train(loss, epochs=0)
The model has 2070091 trainable parameters
# Load pretrained SSDU model for 50 epochs, test on test dataset, and save sample reconstruction
trainer.load_model("models/pretrained/ssdu.pth.tar")

results["noise2inverse"] = trainer.test(test_dataloader)

physics.update_parameters(**params)
results["noise2inverse"]["sample"] = trainer.model(y, physics)

Test results:
PSNR no learning: 26.897 +- 2.730
PSNR: 26.282 +- 2.030

3c. Weighted-SSDU

The Weighted-SSDU [10] loss frames SSDU [6] as a Bernoulli-noise special case of Noisier2Noise [11] and propose a weighting to the SSDU loss to improve SSDU:

\(\mathcal{L}_\text{Weighted-SSDU}=(1-\mathbf{K})^{-1/2}\mathcal{L}_\text{SSDU}\)

where \(\mathbf{K}\) depends on the PDF of the measurement mask \(M\) and the splitting mask \(M_1\).

[10] Millard C. & Chiew M., “A theoretical framework for self-supervised MR image reconstruction using sub-sampling via variable density Noisier2Noise”
[11] Moran N. et al., “Noisier2Noise: Learning to Denoise from Unpaired Noisy Data”

split_generator = dinv.physics.generator.GaussianMaskGenerator(img_size=(128, 128), acceleration=2, rng=rng, device=device)

loss = dinv.loss.WeightedSplittingLoss(
    mask_generator=dinv.physics.generator.MultiplicativeSplittingMaskGenerator((1, 128, 128), split_generator),
    physics_generator=physics_generator
)
# Set epochs > 0 to train the model
trainer = train(loss, epochs=0)
The model has 2070091 trainable parameters
# Load pretrained model for 50 epochs, test on test dataset, and save sample reconstruction
trainer.load_model("models/pretrained/weighted-ssdu.pth.tar")

results["weighted-ssdu"] = trainer.test(test_dataloader)

physics.update_parameters(**params)
results["weighted-ssdu"]["sample"] = trainer.model(y, physics)

Test results:
PSNR no learning: 26.897 +- 2.730
PSNR: 26.780 +- 1.295

4. Other methods

We have numerous other self-supervised learning methods implemented in DeepInverse and benchmarked in “Benchmarking Self-Supervised Methods for Accelerated MRI Reconstruction”, including:

[12] Bora A., Price E. & Dimakis A., “AmbientGAN”
[13] Pajot A., de Bezenac E., Gallinari P., “Unsupervised Adversarial Image Reconstruction”
[14] Cole E. et al., “Fast Unsupervised MRI Reconstruction … Using GANs”
[15] Darestani M. & Heckel R., “Accelerated MRI with Un-trained Neural Networks”
[16] Tachella J., Davies M. & Jacques L., “UNSURE”

5. Baselines

We also provide an upper-limit experiment using oracle supervised learning…

\(\mathcal{L}_\text{sup}=\lVert\hat x-x\rVert_2^2\)

…and a naive unsupervised baseline using only measurement consistency:

\(\mathcal{L}_\text{MC}=\lVert A\hat x-y\rVert_2^2\)

trainer = train(dinv.loss.SupLoss(), epochs=0)
trainer.load_model("models/pretrained/sup.pth.tar")
results["sup"] = trainer.test(test_dataloader)
physics.update_parameters(**params)
results["sup"]["sample"] = trainer.model(y, physics)
The model has 2070091 trainable parameters
Test results:
PSNR no learning: 26.897 +- 2.730
PSNR: 31.779 +- 2.595

trainer = train(dinv.loss.MCLoss(), epochs=0)
trainer.load_model("models/pretrained/mc.pth.tar")
results["mc"] = trainer.test(test_dataloader)
physics.update_parameters(**params)
results["mc"]["sample"] = trainer.model(y, physics)
The model has 2070091 trainable parameters
Test results:
PSNR no learning: 26.897 +- 2.730
PSNR: 26.896 +- 2.730

6. Side-by-side comparison

Note: these results are for a toy problem on 128x128 images trained for 50 epochs. For full benchmark results on full datasets see the paper “Benchmarking Self-Supervised Methods for Accelerated MRI Reconstruction”.

import pandas as pd
pd.DataFrame.from_dict(results, orient="index", columns=("PSNR", "PSNR no learning")).sort_values('PSNR', ascending=False).round(3).transpose()
sup mo-ei diffeo-ei moi ei mc ssdu noise2inverse
PSNR 31.779 31.601 31.388 31.260 30.643 26.896 26.796 26.282
PSNR no learning 26.897 26.897 26.897 26.897 26.897 26.897 26.897 26.897

6. Side-by-side comparison

Note: these results are for a toy problem on 128x128 images trained for 50 epochs. For full benchmark results on full datasets see the paper “Benchmarking Self-Supervised Methods for Accelerated MRI Reconstruction”.

dinv.utils.plot({f"{k}: {round(v['PSNR'], 2)} dB": v['sample'] for (k, v) in results.items()})

7. Summary

Method Implementation
MC dinv.loss.MCLoss()
SSDU dinv.loss.SplittingLoss(eval_split_input=False)
Noise2Inverse dinv.loss.SplittingLoss(eval_split_input=True)
Weighted-SSDU dinv.loss.WeightedSplittingLoss()
Adversarial dinv.loss.UnsupAdversarialGeneratorLoss()
UAIR dinv.loss.UAIRGeneratorLoss()
VORTEX dinv.loss.VORTEXLoss()
EI dinv.loss.EILoss()
MOI dinv.loss.MOILoss()
MO-EI dinv.loss.MOEILoss()

Citation

If you found this useful, please cite the paper using:

@misc{wang2025benchmarking,
      title={Benchmarking Self-Supervised Methods for Accelerated MRI Reconstruction}, 
      author={Andrew Wang and Mike Davies},
      year={2025},
      eprint={2502.14009},
      archivePrefix={arXiv},
      primaryClass={eess.IV},
      url={https://arxiv.org/abs/2502.14009}, 
}

andrewwango.github.io/deepinv-selfsup-fastmri