Tutorial: Fundamentals of transformers

Vision Transformer high level
Results
Components
a. Self attention
b. Positional encoding
Modern transformers
a. Group equivariant transformers
b. Shifted window vision transformers

1. Vision Transformer high level

transformer = tokenisation + embedding + transformer encoder + task-specific “head”

For now, ignore details about the encoder and positional encoding.

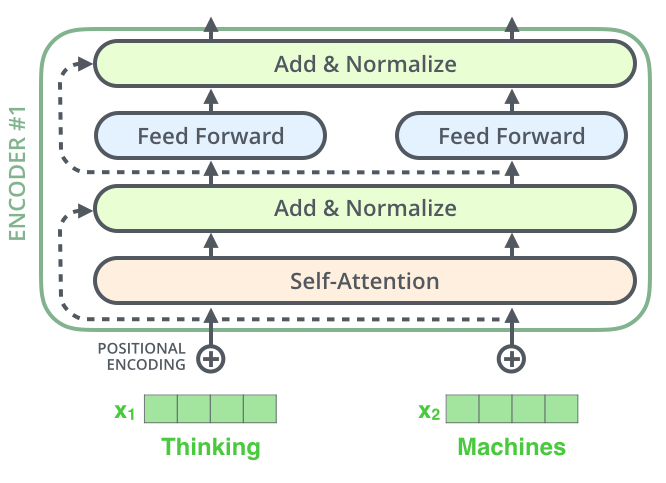
From The Illustrated Transformer

Vision transformer: only the tokeniser changes: patch-based tokenisation. Everything else equivalent.

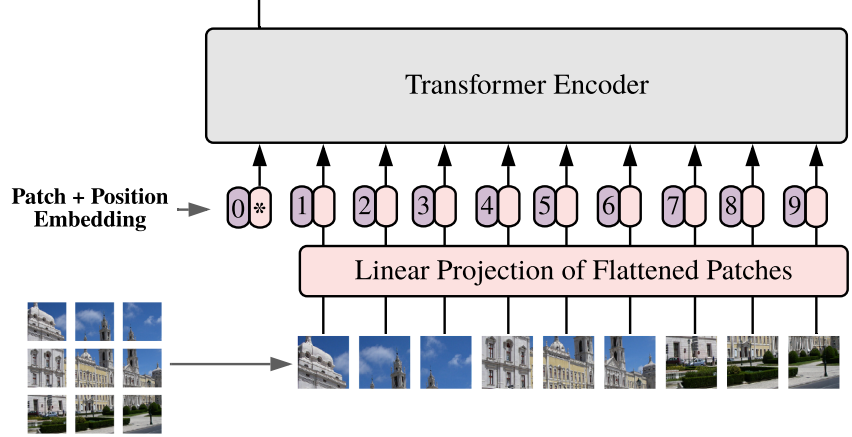
From Dosovitsky et al. An image is worth 16x16 words: transformers for image recognition at scale.

Transformer encoder = self-attention + MLP (+ layernorm + skip connections)

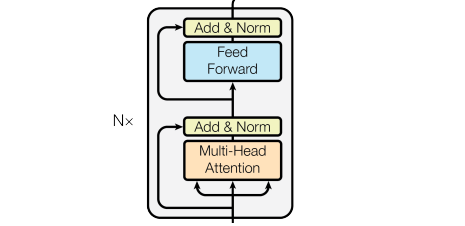
From Vaswani et al. Attention is all you need

Task specific head can be…

Classification: MLP
Image reconstruction: convolutional layer (e.g. swinIR, swinMR)
Autoregressive tasks: transformer decoder with masked self-attention and cross-attention
- Autoregressive machine translation better than non-autoregressive
- Questionable with images: Cao et al. The Image Local Autoregressive Transformer

2. Results

Example application: Lin et al. ViT enable fast and robust accelerated MRI

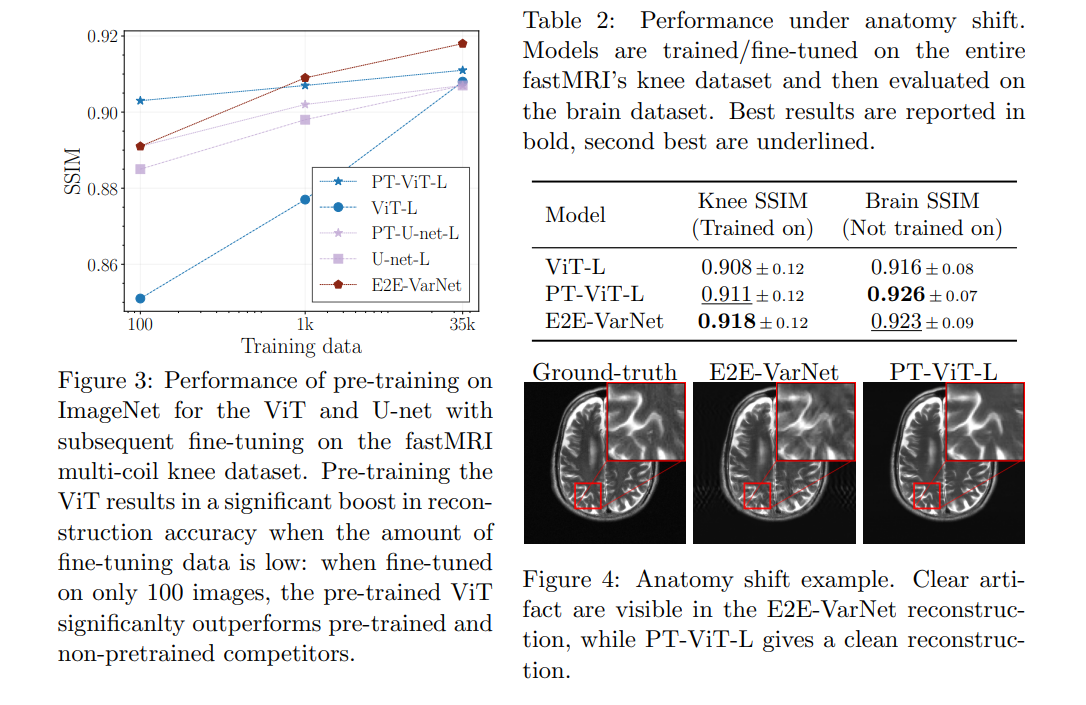
Compare performances wrt. pretraining performance, distribution shift.

3a. Self attention

Skip to 3:29: Attention

Self-attention matrix equations - taken from Romero et al. Group equivariant stand-alone self-attention for vision

Let rows of \(\mathbf{X}\) be vectors representing patch embeddings.
\(\text{SA}(X)=\text{softmax}(\mathbf{Q}\mathbf{K}^T)\mathbf{V}=\text{softmax}(\mathbf{X}\mathbf{W}_Q(\mathbf{X}\mathbf{W}_K)^T)\mathbf{X}\mathbf{W}_V\)

dimensional normalising terms; where \(\mathbf{W}_{{Q,K,V}}\) learnable.

Multi-head self-attention: self-attention performed \(h\) times with \(h\) different \(\mathbf{W}_{{Q,K,V}}\) matrices, output concatenated and passed through one FC layer.

Advantages over convolution operation

Convolution kernel constant across image, whereas now both “kernel” and impact of self-attention depends on the patch.
Now each layer can model long-range dependencies

3b. Positional encodings

See above video. Skip to 7:55

Summary:

Positional encoder takes patch position \(i\) e.g. \(i={1..9}\) and outputs a vector to be summed to embedding vector.
Positional encoder can either be fixed (according to a complicated scheme) or learned.

Dosovitsky et al. - Position embeddings are added to the patch embeddings to retain positional information. We use standard learnable 1D position embeddings, since we have not observed significant performance gains from using more advanced 2D-aware position embeddings

Absolute positional encoding (taken from Romero et al.)

\(\text{SA}(x)=\text{softmax}(\mathbf{A})\mathbf{X}\mathbf{W}_V;\quad\mathbf{A}= (\mathbf{X}+\mathbf{P})\mathbf{W}_Q((\mathbf{X}+\mathbf{P})\mathbf{W}_K)^T\)

“Relative” positional encoding

Introduced by Shaw et al. (2018), relative encodings consider the relative distance between the query token \(i\) (the token we compute the representation of), and the key token \(j\) (the token we attend to). The calculation of the attention scores then becomes:

\(\mathbf{A}{i,j}=\mathbf{X}_i\mathbf{W}_Q((\mathbf{X}_j+\mathbf{P}{x(j)-x(i)})\mathbf{W}_K)^T\)

Aside: learned positional encodings experiments

Dosovitsky et al. - As we can see, while there is a large gap between the performances of the model with no positional embedding and models with positional embedding, there is little to no difference between different ways of encoding positional information. We speculate that since our Transformer encoder operates on patch-level inputs, as opposed to pixel-level, the differences in how to encode spatial information is less important. More precisely, in patch-level inputs, the spatial dimensions are much smaller than the original pixel-level inputs, e.g., 14 × 14 as opposed to 224 × 224, and learning to represent the spatial relations in this resolution is equally easy for these different positional encoding strategies.

Inductive bias: Dosovitsky et al. - We note that Vision Transformer has much less image-specific inductive bias than CNNs. In CNNs, locality, two-dimensional neighborhood structure, and translation equivariance are baked into each layer throughout the whole model. In ViT, only MLP layers are local and translationally equivariant, while the self-attention layers are global. The two-dimensional neighborhood structure is used very sparingly: in the beginning of the model by cutting the image into patches and at fine-tuning time for adjusting the position embeddings for images of different resolution (as described below). Other than that, the position embeddings at initialization time carry no information about the 2D positions of the patches and all spatial relations between the patches have to be learned from scratch.

4a. Group equivariant transformers

Romero et al. Group equivariant stand-alone self-attention for vision:

Positional encodings that are G-equivariant impose G-equivariance of the whole transformer
Self-attention without positional encodings is permutation invariant
To more specifically impose other equivariances:
- Translation: use relative positional encoding
- Rotation: impose that positional encoding equal for all rotations
Don’t perform as well as G-CNNs…

Question: can group equivariance properties of positional encoding be framed in the context of EI?

Probably not - since positional encoding acts on input images \(A^\dagger x\) rather than the actual images \(x\)?

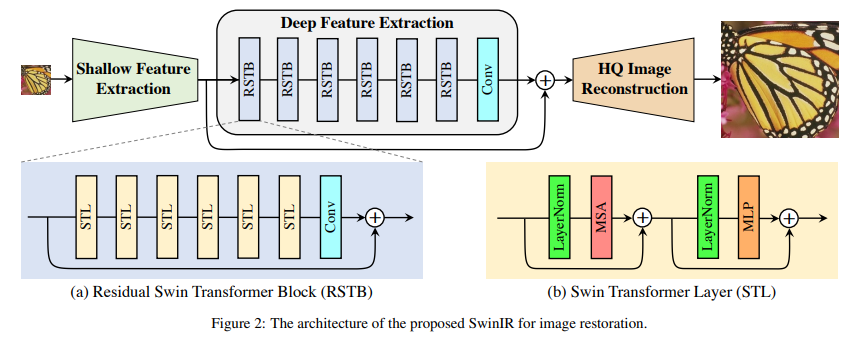
4b. Swin

Liang et al. (swinIR paper) - Recently, Swin Transformer has shown great promise as it integrates the advantages of both CNN and Transformer. On the one hand, it has the advantage of CNN to process image with large size due to the local attention mechanism. On the other hand, it has the advantage of Transformer to model long-range dependency with the shifted window scheme.

Liu et al. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows

Skip to 6:51 Swin Transformer Block